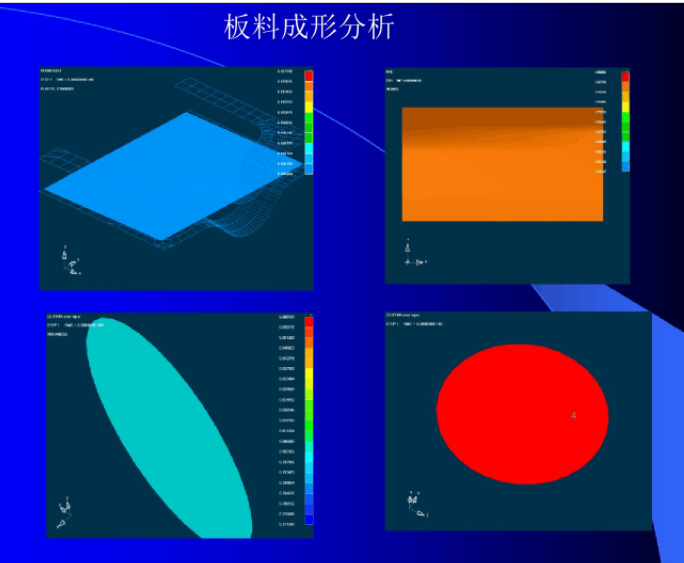
序言
长期以来，成形工艺和模具的设计以及工艺过程剖析主要是依据堆集的实践经验、行业标准和传统理论进行。但由于实践经验的非确定性、行业标准的时效性、而传统理论对变形条件和变形过程进行了简化;因而，对复杂的成形工艺和模具设计往往不容易取得满意的成果，使得调试模具的时刻长、次数多，甚至导致模具的报废。通常情况下，保证工艺和模具的可靠与安全，多选用保守的设计方案，形成工序的增多，模具结构尺寸的加大。
CAE所涉及的内容非常丰富，泛指运用科学的办法、以计算机软件的办法，为工程领域提供一种有用的辅助工具，帮助工程技术人员对产品、加工工艺、工模具、以及制形成本等进行反复的评估、修改和优化，直到取得最佳的成果。但由于所开发CAE软件的品种、功用都较有限，系列化与集成化都难以实现;因而，CAE使用还远未达到所定义规模。现在，模具CAE的主要内容还仅仅是利用CAD生成的模型进行成形工艺过程的数值模拟，以取得成形工件内不一起刻恣意方位的应力应变等多种场量的分布情况以及潜在的问题等其它相关信息;并经过剖析研究这些信息，以达到以下几个方面的主要目的:
1、对工件的可加工性能作出早期的判断，预先发现成形中或许发生的质量缺陷，并模拟各种工艺方案，以削减模具调试次数和时刻，缩短模具开发时刻;
2、对模具进行强度刚度校核，择优选取模具资料，猜测模具的损坏办法和模具的寿数，进步模具的可靠性，降低模具成本;
3、经过仿真进行优化设计，以取得最佳的，工艺方案和工艺参数，增强工艺的稳定性、降低资料消耗、进步生产功率和品的质量;
4、查找工件质量缺陷或问题发生的原因，以寻求合理的解决方案。
名成形过程数值模拟是模具CAE中的基础，现在所选用的数值模拟办法主要有两种:有限元法和有限差分法;一般在空间上选用有限元办法，而当涉及到时刻时，则运用有限差分法。以下扼要介绍有关数值模拟的基本内容和办法。
广州软件开发公司业务咨询卢先生 手机18998818351 售后服务热线：020-22076940
